Insiemi

In matematiche, un insiemi (insieme par talian e set par inglês) al è une colezion di ogjets che e ven considerade come un dutun. Cheste idee, inte sô semplicitât, e je a la base di ducj i cjamps de matematiche tant che il prin cjapitul di cualsisei bon libri di test al è dedicât al studi des principâls carateristichis e proprietâts dai insiemis.

In chest articul si cjatin lis basis de teorie classiche dai insiemis, dite ancje intuitive o naïve. No si cjaparà in considerazion, invezit, la moderne teorie assiomatiche.

Definizions

Un insiemi al è une colezion di ogjets, che a vegnin clamâts elements dal insiemi. I elements a definissin totalmentri un insiemi: par esempli, si dîs che l'insiemi $A$ e l'insiemi $B$ (l'ûs des letaris maiusculis par clamâ i insiemis al è une vore comun) a son compagns se e dome se a son costituîts dai stes elements; in chel câs si pues scrivi $A=B$.

Intal stes insiemi si puedin vê ogjets di nature diferente (par esempli un flôr, un numar e un libri). Dâts un insiemi $A$ e un ogjet $a$, si pues verificâ un e dome un dai doi câs che a seguissin:

1. $a$ al è un element di $A$: a si dîs che $a$ al aparten a $A$ e si scrîf $a\in A$;
2. $a$ nol è un element di $A$: a si dîs che $a$ nol aparten a $A$ e si scrîf $a\notin A$.

Chest al impliche che:

• no esistin câs intermedis: un element o al aparten o nol aparten a un insiemi;
• un element nol pues jessi ripetût: se al aparten a un insiemi alore al è unic inta chel insiemi.

Descrizion

Definî un insiemi al significhe specificâ cuai che a son i elements che lu componin e lis dôs manieris par fâlu a son:

1. par liste, o sei disint un a un ducj i elements:
   $A=\{0;7;33;10088\}=\{10088;7;0;33\};$
   $B=\{{\mbox{garofui; patatis; trisculis; cjariesis}}\};$
   Lis dôs definizions di $A$ a son ecuivalentis: l'ordin dai elements nol conte;
2. par carateristiche, o sei spiegant a peraulis cuale che e je la propietât che a lee ducj i elements:
   $C=\{{\mbox{i numars pari}}\};$
   $D=\{{\mbox{lis machinis cuntune ruede sbuse}}\}.$
   In câs plui complicâts, lis descrizions a puedin jessi dal tipo
   $C=\{\forall n\in \mathbb {N} :n=2m,\forall m\in \mathbb {N} \}$
   $E=\{\forall (x,y)\in \mathbb {R} ^{2}:y=3x+5\}.$
   Ancje chi, $C$ al è il stes insiemi intai doi câs (il significât dai simbui $\mathbb {N}$ e $\mathbb {R}$ al sarà spiegât plui indevant).

Cardinalitât

Il numar di elements di un insiemi si clame la cardinalitât dal insiemi. Cun riferiment ai esemplis precedents, la cardinalitât dai insiemis $A$ e $B$ e je di 3 e 4 rispetivementri. Chescj a son esemplis di di insiemis finîts, che a son costituîts, vâl a dî, di un numar finît di elements; $C$ e $E$ a son invezit insiemis infinîts e a àn cardinalitât infinide (plui detais sui insiemis cuntun numar infinît di elements tal articul su la cardinalitât).

L'insiemi di cardinalitât 0 (cun nissun element) si dîs insiemi vueit e si indiche cun il simbul $\emptyset$.

Insiemis numerics fondamentâi

Introdusin cumò i insiemis numerics plui usâts in matematiche.

• I numars naturâi a son ducj i intîrs no negatîfs:
  $\mathbb {N} =\{0;1;2;3;4;...\}.$
• I numars intîrs relatîfs, vâl a dî cun segn, si indichin cun $\mathbb {Z}$
  $\mathbb {Z} =\{...;-3;-2;-1;0;1;2;3;...\}.$
• $\mathbb {Q}$ al è l'insiemi dai numars razionâi, ven a stai di dutis lis frazions iridusibilis (in realtât, lis frazions 3/4 e 6/8, dome par fâ un esempli, a rapresentin il stes numar) positivis e negativis:
  $\mathbb {Q} =\{\forall q:q={\frac {m}{n}},\forall m,n\in \mathbb {Z} {\mbox{ e }}n\neq 0\}$.
• L'insiemi di ducj i numars decimâi cuntun numar di cifris decimâi finît, infinît periodic o infinît no periodic a si clame insiemi dai numars reâi $\mathbb {R}$.
• I numars complès $\mathbb {C}$ a son une astrazion matematiche definide par podê risolvi cierts problemis. Clamant $i={\sqrt {-1}}$ la unitât imagjinarie, si à
  $\mathbb {C} =\{\forall z:z=x+iy,\forall x,y\in \mathbb {R} \}$.

Relazions tra insiemis

Si à za dit che doi insiemis cui stes elements a son il stes insiemi: in tal câs si pues ancje dî che i doi insiemis a son coincidents. Al contrari, doi insiemis che no àn nissun element comun a si disin disiunts.

Sotinsiemis

$A$ al è un sotinsiemi di $B$.

L'insiemi $B$ al è un sotinsiemi dal insiemi $A$ se e dome se ducj i elements di $B$ a son ancje elements di $A$. La scriture doprade e je

$B\subseteq A{\mbox{ o ancje }}A\supseteq B$.

Se si è sigûrs che $A$ al vedi ancje elements che no apartegnin a $B$, si tabaie alore di sotinsiemi tal sens stret o sotinsiemi propri e si scrîf:

$B\subset A{\mbox{ o ancje }}A\supset B$.

Si à di notâ che cualsisei insiemi al à almancul doi sotinsiemis impropris (no tal sens stret): l'insiemi vueit $\emptyset$ e l'insiemi stes.

Par i insiemis numerics fondamentâi viodûts inte sezion anteriôr, a valin lis relazions che a seguissin:

$\mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C}$.

(Nol è un erôr scrivi $\mathbb {N} \subseteq \mathbb {Z} \subseteq \mathbb {Q} \subseteq \mathbb {R} \subseteq \mathbb {C}$.)

Insiemi des parts

L'insiemi di ducj i sotinsiemis di un insiemi $A$ si clame insiemi des parts (en:power set in inglês) di $A$. Par esempli, se $A=\{1,2,3\}$, l'insiemi des parts ${\mathcal {P}}(A)$ al è

${\mathcal {P}}(A)=\{\emptyset ;A;\{1\};\{2\};\{3\};\{1;2\};\{1;3\};\{2;3\}\}$.

Par un insiemi finît di $n$ elements, si pues dimostrâ che la cardinalitât dal insiemi des parts e je $2^{n}$ (in curt, par ogni element a son dôs pussibilitâts: che al stedi o che nol stedi tal sotinsiemi considerât. Une volte decidût se un element al sta o no tal sotinsiemi, si à di fâ compagn par ducj chei altris elements. Il numar di pussibii sotinsiemis si calcole duncje moltiplicant un fatôr 2 par ogni element).

Operazions cui insiemis

Union di doi insiemis.

Intersezion di doi insiemis.

Insiemi diference di doi insiemis.

Complementâr dal insiemi $A$ intal insiemi univiers $U$.

• Union: la union di doi insiemis al è un insiemi che al conten sie i elements dal prin insiemi che chei dal secont. Par esempli, se definin
  $A=\{1;4;8;11\}{\mbox{ e }}B=\{3;5;4;7;1\}$
  alore la union e je
  $A\cup B=\{1;4;8;11;3;5;7\}$.
  Si pues notâ che $A$ e $B$ a son sotinsiemis dal insiemi union $A\cup B$ e che i elements comuns ai doi insiemis ($\{1;4\}$) no vegnin ripetûts.

• Intersezion: la intersezion di doi insiemis e je un insiemi che al à come elements dome i elements comuns ai doi insiemis. Cun $A$ e $B$ come prime, si à
  $A\cap B=\{1;4\}$.
  De definizion, al risulte clâr che l'insiemi intersezion al è un sotinsiemi di ducj i doi i insiemis di partence.
  O vin viodût prime che doi insiemis si disin disgiunts cuant che no àn elements in comun. Si pues cumò dâ une definizion ecuivalent e disi che doi insiemis a son disgiunts se la lôr intersezion e da un insiemi vueit.

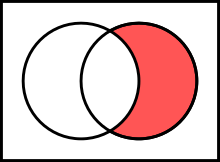
• Insiemi diference: l'insiemi diference di $A$ in $B$ ($B\setminus A$ o $B-A$) al è l'insiemi dai elements di $B$ che no apartegnin a $A$. Continuant cul esempli:
  $B\setminus A=\{3;5;7\}{\mbox{ e }}A\setminus B=\{8;11\}$.

• Complementâr: In cierts câs, ducj i insiemis considerâts a son sotinsiemis di un insiemi plui grant clamât insiemi univiers; in chestis situazions, il complementâr di un insiemi $A$ al è l'insiemi diference di $A$ intal insiemi univiers. Se o clamìn $U$ l'insiemi univiers e ${\bar {A}}$ (o ancje ${\mathcal {C}}_{U}(A)$ o $A'$) il complementâr di $A$, si à
  ${\bar {A}}=U\setminus A$.

• Prodot Cartesian: I elements dal prodot cartesian $A\times B$ di doi insiemis $A$ e $B$ a son dutis lis pussibilis copis ordenadis che si puedin costruî sielzint il prin element intal insiemi $A$ e il secont element intal insiemi $B$. In simbui:
  $A\times B=\{(a,b)|a\in A{\text{ e }}b\in B\}.$
  Al e facil viodi che la cardinalitât dal prodot cartesian $A\times B$ e je il prodot des cardinalitâts di $A$ e $B$ (cuant che $A$ e $B$ a an un numar finît di elements). Cun di plui, jessint che i elements di $A\times B$ a son copis ordenadis, il prodot cartesian nol è comutatîf, vâl a dî $A\times B\neq B\times A$.

Proprietâts des operazions

Presentìn cumò lis principâls proprietâts des operazions cui insiemis. Intai esemplis che a seguissin, i insiemis $A,B$ e $C$ a son sotinsiemis dal insiemi univiers $U$.

• Proprietât comutative: union e intersezion a gjoldin de proprietât comutative
  $A\cup B=B\cup A$;
  $A\cap B=B\cap A$.
• Proprietât associative: union e intersezion a gjoldin de proprietât associative, che e permet di estindi la definizion des dôs operazions ai câs cun plui di doi insiemis
  $A\cup B\cup C=(A\cup B)\cup C=A\cup (B\cup C)$;
  $A\cap B\cap C=(A\cap B)\cap C=A\cap (B\cap C)$.
• Proprietât distributive: de intersezion rispiet ae union
  $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$
  e de union rispiet ae intersezion
  $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$.
• Formulis di De Morgan:
  ${\overline {A\cap B}}={\bar {A}}\cup {\bar {B}}$;
  ${\overline {A\cup B}}={\bar {A}}\cap {\bar {B}}$.

A valin, par prionte, ancje lis seguintis proprietâts cence un non particolâr:

• $A\cup A=A{\mbox{ e }}A\cap A=A$;
• $A\cup \emptyset =A{\mbox{ e }}A\cap \emptyset =\emptyset$;
• ${\overline {\bar {A}}}=A$;
• $A\cap {\bar {A}}=\emptyset {\mbox{ e }}A\cup {\bar {A}}=U$;
• $A\setminus A=\emptyset$;
• $A\setminus B=A\cap {\bar {B}}$.

Bibliografie

• G. Spirito. Matematica Senza Numeri. Newton Compton, 1995. ISBN 88-7983-814-8
• A. M. Pittana, G. Mitri e L. De Clara. La Nomencladure des Matematichis. Istitût Ladin Furlan Pre Checo Placerean, 1997.
• M. Fogale e E. Paolini. Une Introduzion ae Analisi Matematiche. Istitût Ladin Furlan Pre Checo Placerean, 2001.
• Wikipedia Contributors. Set, in Wikipedia, the Free Enciclopedia, 30 July 2007, 00:14 UTC, <http://en.wikipedia.org/w/index.php?title=Set&oldid=147952691> [accessed 9 August 2007]
• Contributori di Wikipedia. Insieme, in Wikipedia, l'Enciclopedia Libera, 8 giugno 2007, 19:50 UTC, <http://it.wikipedia.org/w/index.php?title=Insieme&oldid=9201617> [in data 9 agosto 2007]